Случайные числа не случайны

Случайные числа не случайны. Вы когда-нибудь задумывались, как работает Math.random ()? Что такое случайное число и как его получить? И представьте себе вопрос на собеседовании: напишите свой

Случайные числа не случайны

Вы когда-нибудь задумывались, как работает Math.random ()? Что такое случайное число и как его получить? Представьте себе вопрос для собеседования: напишите свой генератор случайных чисел в пару строк кода. Так что это, случайность и ее можно предсказать.

Генератор псевдослучайных чисел и генератор случайных чисел

Чтобы получить что-то случайное, нам нужен источник энтропии, источник хаоса, из которого мы будем генерировать случайность.

Этот источник используется для накопления энтропии с последующим получением от него начального (начального) значения, которое необходимо генераторам случайных чисел (ГСЧ) для генерации случайных чисел.

Генератор псевдослучайных чисел использует одно начальное значение, отсюда его псевдослучайность, в то время как генератор случайных чисел всегда генерирует случайное число, начиная с высококачественной случайной величины, которая берется из различных источников энтропии.

Энтропия — это мера беспорядка. Информационная энтропия — это мера неопределенности или непредсказуемости информации.

Получается, что для создания псевдослучайной последовательности нам нужен алгоритм, который генерирует определенную последовательность на основе определенной формулы. Но такую ​​последовательность можно предсказать. Однако давайте представим, как мы могли бы написать собственный генератор случайных чисел, если бы у нас не было Math.random()

PRNG имеет алгоритм, который можно воспроизвести.
ГСЧ полностью получает числа из любого шума, способность вычислять какой из них стремится к нулю. В то же время в ГСЧ есть определенные алгоритмы выравнивания распределения.

Придумываем алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ) — это алгоритм, который генерирует последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному (обычно равномерному) распределению).

Мы можем взять последовательность некоторых чисел и получить модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и какой модуль. Если вы перейдете напрямую от 0 к N и по модулю 2, вы получите генератор 1 и 0:

Эта функция генерирует для нас последовательность 01010101010101 . и вы даже не можете назвать ее псевдослучайной. Чтобы генератор был случайным, он должен пройти проверку на следующий бит. Но у нас нет этой задачи. Однако даже без каких-либо тестов мы можем предсказать следующую последовательность, а это значит, что такой алгоритм не подходит фронтально, но мы идем в правильном направлении.

Но что, если мы возьмем известную, но нелинейную последовательность, например число PI. И в качестве значения для модуля мы возьмем не 2, а что-то другое. Вы также можете думать об изменении значения формы. Последовательность цифр в числе Пи считается случайной. Генератор может работать с числами Пи, начиная с неизвестной точки. Пример такого алгоритма с последовательностью на основе PI и изменяемым модулем:

Но в JS номер PI может отображаться только до 48 символов и не более. Следовательно, такую ​​последовательность по-прежнему легко предсказать, и каждый запуск такого генератора всегда будет давать одни и те же числа. Но наш генератор уже начал показывать числа от 0 до 9. Кстати, вот как выглядит распределение чисел до 10 000 итераций:

Распределение очень нерегулярное, но мы получаем генератор чисел от 0 до 9.

Мы можем взять не число Пи, а время в числовой форме и рассматривать это число как последовательность цифр, и, чтобы последовательность не повторялась каждый раз, мы будем читать ее с конца. В целом наш алгоритм для нашего ГПСЧ будет выглядеть так:

Это уже похоже на генератор псевдослучайных чисел. А Math.random () сам по себе является ГПСЧ, о нем мы поговорим чуть позже. Кроме того, первое число каждый раз разное.

Собственно, используя эти простые примеры, вы можете понять, как работают более сложные генераторы случайных чисел. И есть даже готовые алгоритмы. Например, давайте посмотрим на один из них: это линейный конгруэнтный ГПСЧ (LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ (LCPRNG) — распространенный метод генерации псевдослучайных чисел. Это не является криптографически стойким. Этот метод заключается в вычислении элементов повторяющейся линейной последовательности по модулю натурального числа m, заданного следующей формулой:

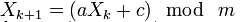
где a (множитель), c (сложение), m (маска) — некоторые целые коэффициенты. Результирующая последовательность зависит от выбора начального числа, например начального числа. Разные начальные значения производят разные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LCPRNG (но не совсем такой алгоритм(!)).

Как было сказано выше, эта последовательность предсказуема. Так зачем нам ГПСЧ? Когда дело доходит до безопасности, проблема с ГПСЧ. Если говорить о других активах, эти свойства могут иметь преимущество. Например, для различных спецэффектов и графической анимации может потребоваться частый вызов наугад. И вот тут важно распределение смыслов и результативность! Вторичные алгоритмы не могут похвастаться скоростью работы.

Другое свойство — воспроизводимость. Некоторые реализации позволяют установить начальное число, что очень полезно, если последовательность необходимо повторить. Воспроизведение необходимо, например, в тестах. И есть много других вещей, которым не нужен безопасный ГСЧ.

Как устроен Math.random()

Метод Math.random () возвращает псевдослучайное число с плавающей запятой из диапазона 0, 1), то есть от 0 (включительно) до 1 (исключая 1), которое затем можно масштабировать до желаемого диапазона. Сама реализация выбирает начальное число для алгоритма генерации случайных чисел; он не может быть выбран или удален пользователем.

Как работает алгоритм Math.random () — интересный вопрос. До недавнего времени, то есть до 49 Chrome, использовался алгоритм MWC1616:

именно этот алгоритм генерирует нам последовательность псевдослучайных чисел в диапазоне от 0 до 1.

Исправлена ​​ошибка в алгоритме MWC1616 (отсутствие скобок). Та же ошибка повторяется в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html

итак, мы видим, что должны быть круглые скобки:

Предсказываем Math.random()

Чем это было чревато? Есть такой поиск: https://alf.nu/ReturnTrue

Что вам нужно написать вместо вопросов, чтобы функция вернула истину? Это кажется невозможным. Но это возможно, если вы посмотрели спецификации и увидели алгоритм V8 PRNG. Роман Дворнов показал мне решение этой проблемы:

Этот код работал в 70% случаев для Chrome <49 и Node.js <5. Рома Дворнов, как всегда, показал чудеса магии, которые являются не чем иным, как глубоким пониманием внутреннего устройства браузеров. Я все еще жду, когда Роман сделает отчет по этим событиям или напишет более подробную статью.

Что тут происходит? Дело в том, что алгоритм предсказуем. Чтобы было понятнее, вы можете сгенерировать изображение со случайным пикселем. На сайте https://bl.ocks.org/mmalone/bf59aa2e44c44dde78ac

есть такой генератор. Вот что произошло, когда алгоритм MWC1616 был в браузере:

Вы видите эти однородности на левом слайде? На изображении показана проблема с распределением значений. На изображении слева видно, что значения кое-где сильно сгруппированы, а кое-где отваливаются большие фрагменты. Следовательно, цифры можно предсказать.

Оказывается, мы можем перевернуть Math.random () и предсказать, какое число было угадано на основе того, что мы получили в любой момент времени. Для этого мы получаем два значения через Math.random (). Затем мы вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние, мы можем предсказать следующие значения Math.random () без изменения внутреннего состояния. Измените код так, чтобы возвращалось предыдущее значение вместо следующего. Фактически, все это описано в коде решения задачи random4. Но затем алгоритм был изменен (подробности читайте в спецификации). Его можно сломать, как только у нас на JS заработает нормальное 64-битное число. Но это будет отдельная история.

Новый алгоритм выглядит так:

Его еще можно будет рассчитать и спрогнозировать. Но пока у нас в JS нет «длинной математики». Вы можете попробовать создать или использовать специальные библиотеки через TypedArray. Может, когда-нибудь кто-нибудь снова напишет гадалке. Может быть, это будешь ты, читатель. Кто знает ?

Сrypto Random Values

Метод Math.random () не предоставляет криптостойкие случайные числа. Не используйте его в целях безопасности. Вместо этого он использует API веб-криптографии (API веб-криптографии) и более точный метод window.crypto.getRandomValues() .

Пример генерации случайного числа:

Но в отличие от PRNG Math.random () этот метод требует много ресурсов. Дело в том, что этот генератор использует системные вызовы в операционной системе для получения доступа к источникам энтропии (MAC-адрес, процессор, температура и т.д.…).

Материалы про Math.random()

Более рандомно в спецификациях:

Хорошая статья о том, как работает рандомизатор

Пример реализации предиктора с Math.random()

Кстати, за обновлениями и другими материалами от меня вы можете следить в Telegram-канале: @prowebit

В этом канале я публикую не только статьи из этого блога, но и различные новости и мысли. Подписывайся ?

Мы расскажем, что такое рандомайзер и чем он может быть полезен. Особенности использования генератора случайных чисел в социальных сетях.

Что такое рандомайзер

Рандомайзер, также известный как генератор случайных чисел, — это сервис, который позволяет вам определять случайного победителя.

В сети есть множество генераторов случайных чисел для розыгрышей, каждый из которых использует специальный алгоритм генерации случайных чисел. Такие генераторы нашли свое применение во многих сферах жизни человека. Они широко используются в области науки, искусства, статистики, криптографии, игр и так далее. Например, случайное распределение в рандомизированных контролируемых испытаниях помогает ученым проверять гипотезы.

Для определения этого понятия нельзя не вспомнить такой термин, как «случайный», пришедший к нам с другой стороны океана. В буквальном переводе на русский язык «случайный» означает «случайный», «произвольный», «хаотичный». Само слово «казуальный», скорее всего, вошло в новый русскоязычный молодежный сленг благодаря игровому сообществу. Вспомните хотя бы пиксельные РПГ, где в выпадении игровых значений, полученных игроками после убийства мобов или других игроков, был элемент случайности. В современных ролевых играх и MMORPG принцип остается прежним.

У этого термина есть и другие значения, см. Генератор случайных чисел. Генератор псевдослучайных чисел (PRNG, англ. Pseudo-random number generator,…

Генерация случайных чисел в Python

Давайте рассмотрим наиболее распространенный вариант использования модуля: создание случайного числа. Чтобы получить случайное целое число, Python использует функцию .

Следующие две функции могут использоваться для генерации случайных целых чисел:

В следующем примере показано, как получить случайно сгенерированное число от 0 до 9.

из случайного импорта randint

print («Вывести случайное целое число», randint (0, 9))
print («Вывести случайное целое число», randrange (0, 10, 2))

print («Вывести случайное целое число», randint (, 9))

print («Вывести случайное целое число», randrange (, 10,2))

Выдача случайного целого числа 5
Выдача случайного целого числа 2

В следующих разделах статьи будут рассмотрены другие способы генерации случайного числа в Python.

Что такое случайность в игре? Если вы хотите знать все о случайности, вам не обязательно быть игроком, как многие считают. Дело в том, что это понятие скорее относится к компьютерам в целом,

Рандом

Вкратце Генератор случайных чисел в играх.

Сам Великий Бог Случайности

z: Еще у него есть бабушка Ивент, которая всю неделю нас радует.

Большинство настольных и компьютерных игр без случайности скучны.

Во-первых, очень сложно разработать правила, по которым игра будет рассчитываться с большим трудом, так что в большинстве ситуаций есть по крайней мере два хода, которые одинаково полезны для игрока или, по крайней мере, кажутся полезными; очень быстро находят идеальную стратегию, позволяющую добиться максимального результата, которого нельзя добиться никаким другим способом.

Самый известный пример — это, наверное, крестики-нолики. Во-вторых, если игрок хочет играть в шахматы, он может внезапно сыграть в шахматы, а не в жалкую пародию на это. В конце концов, шахматы имеют долгую историю развития от приземленного варгейма до абстрактной, но динамичной игры. Большинство игроков просто хотят убить время с интересом.

Но если вы добавите перемешанные карты или бросок кубика, все сразу станет более разнообразным: например, персонаж стреляет во врага, но промахивается. Или корабли во флоте, контролируемом игроком, не получают сигнал с подветренной стороны. Или наоборот, игрок «купил» два туза или ударил противника по голове.

Все это называется рандом, от английского casual — «кэжуал». Случайность означает непредсказуемость, но статистику — другими словами, игральная кость случайна, а решение оппонента — нет. Конечно, только если это идеальный противник или хотя бы достаточно опытный, конечно; Новички склонны принимать опрометчивые и необоснованные решения, которые временами сбивают с толку профессионалов.

Источники случайности в настольных играх[править]

Игральные кости для ролевых игр. Верхний ряд: додекаэдр (d12), икосаэдр (d20). Второй ряд: икосаэдр (d20), два декаэдра для десятков и единиц (d10 / d100), икосаэдр (d20). Нижний ряд: тетраэдр (d4), два куба (d6), октаэдр (d8).

Наиболее часто используемые кости. В роли игральной кости обычно выступают правильные многогранники или близкие к ним геометрические тела.

Основная статья: нестандартные кости

• Одно из двух: кубики дешевле монеты, поэтому они обычно используют четные или нечетные кубики.
• Один из трех-пяти — т. Н. «Сискин», призма с закругленным основанием (потому что она должна упасть на бок).
• Один из четырех — тетраэдр. Тетраэдр падает вершиной вверх, поэтому отмечены не грани, а вершины. Или рисуют по краям три числа, берется тот, который стоит прямо. Реже октаэдр, в котором пара граней помечена цифрой, удобнее (лучше катится), но DnD также имеет обычный октаэдр d8.
• Один из шести — куб. Те же кости. Куб — самый удобный из многогранников: его легко сделать, он хорошо катится, быстро успокаивается и читается даже при встрече с препятствием. Поэтому игровые дизайнеры стараются адаптировать механику под куб.
  • Также могут быть варианты куба, которые обеспечивают каждый третий, каждый четвертый. Если одно из трех, было два лица с каждым значением. Произведено в СССР, например, в игре «Ягоды» из набора «Три цыпленка» (Издательство «Малыш», 1982 г.). В параметрах «одно из четырех» (из пяти) добавлялись «перевернутые» грани или дублировались два (одно) значения. В СССР / России мы время от времени встречались в журнальных играх «тяни и двигай» в форме зачистки. Я имею в виду, для того, чтобы сделать это самому.

  Также они используют колоду карт или спиннер (волчок, рулетку). В частности, настольные ролевые системы Deadlands и Savage Worlds известны тем, что используют карты; а в первом случае разыгрывание заклинаний обычно моделируется на основе покерных комбинаций.

  Так как даже в обычных играх вы должны выбрать, кто начинает или через какую дверь играть, они используют, чтобы подбросить монетку себе на пальцы, «угадать, из какой руки» или «угадать, с какой стороны идет секундная стрелка».

  В компьютерных играх[править]

  Настольные ролевые игры в основном казуальные. Из них они были случайным образом включены в CRPG. На самом деле случайность используется везде, даже в шутерах. Просто стрелок «испытывает удачу» почти дюжину раз в секунду, и центральная предельная теорема работает, гарантируя небольшой общий разброс. Но в ролевых играх (настольных и компьютерных), где случайность часто решает, взорвалась бомба или была обезврежена, была критическая или нет, неудачная случайная игра вызывает много злоупотреблений [3].

  Если компьютерный генератор случайных чисел неисправен — например, он имеет сильную последовательную корреляцию — его называют корейским случайным, в честь корейской MMORPG, в которой он стал «притчей во языцех».

  Даже если случайность является наиболее случайной и независимой, раз в год может случиться, что три или четыре последовательных критерия упадут [4], и Пуассон изучил статистику таких событий.

  Однако корейские казуальные ролевые игры настолько наскучили, что иногда статистику искусственно сглаживают: если в прошлый раз был критик, то в следующий раз шанс критика уменьшится; если же, наоборот, давно не было, вероятность возрастает [5].

  Цифровые компьютеры устроены так, что один и тот же код с одинаковыми данными дает одинаковый результат. Поэтому для случайных чисел низкого качества, подходящих для некоммерческих игр, используется непредсказуемый алгоритм. Однако это алгоритм и, следовательно, он детерминирован, поэтому его предсказуемость используется с пользой. Мы запускаем генераторы на двух машинах с одним и тем же начальным значением — и они будут выдавать одинаковые числа (это то, на чем основан многопользовательский режим Doom [6]). Эта предсказуемость используется в Elite, позволяя числу записывать целую галактику, аналогичный принцип применяется к Spore.

  Случайность и данмаку — плохая комбинация (игра: Я хочу убить Камилию 3).

  Вызвать случайную бурю негодования в играх Paradox Interactive: какой бы сильной ни была ваша армия, все равно ничего, если кубик будет «1 на 6». Очень яркий пример «Сан Рандомиус».

  В общем, можно выделить критерий, который отличает случайное хорошее от плохого. Хороший выглядит так: «Вот проблема, которая вас бросила наугад, подумайте, как ее исправить». Плохо: «Это случайная проблема, вы ничего не можете с этим поделать, нажмите перезапуск».

  Когда необходимы высококачественные случайные числа (например, в криптографии или азартных играх), они ищут источники реальной случайности, например таймеры, счетчики команд, движения мыши. Лучшим источником считается выброс частиц радиоактивных веществ.

  Терминология, связанная с рандомом[править]

  Cubic thrower — игра, в которой вам нужно часто и в большом количестве бросать кости. Для таких игр есть даже артефакт — кубическая башня, чтобы кубики никуда не катились и не портили игровую среду.

  Сан Рандомиус — когда победа или поражение слишком сильно зависят от случая.

  2d6 + 1 — характерное обозначение формул, непонятное для совершенно не знакомых с настольными играми. Это означает бросание двух шестигранных кубиков и прибавление 1 к общей сумме».

  Источники

  • https://tech.geekjob.ru/js-random-engine/
  • https://stimylrosta.com.ua/voprosy-i-otvety/282-chto-takoe-randomajzer
  • https://searchtips.ru/randomno/
  • https://imp-ustlab.ru/chto-takoe-random-v-igre/